EPM and Methodology

Overview

Dunks and Threes rates NBA players and teams, and predicts games, for every day of basketball since the 2001-02 season. Everything rests on two predictions made for each player each day:

• Estimated Skills: the player's true level in each stat, such as 3-point percentage or turnover rate, separated from random variation.
• Estimated Plus-Minus (EPM): the player's predicted contribution to the team, in points per 100 possessions.

The rest of the site builds on these:

• Expected EPM predicts a player's impact as of a date.
• Actual EPM rates a season from the games actually played.
• Team ratings combine player EPM with each player's expected minutes.
• Game predictions, box score projections, and season simulations play those ratings forward.
• Estimated Game Production (EGP) measures what a single box score line was worth.

Everything updates nightly. Figures on this page are as of October 2026.

Methodology

The Need for Adjustment to Plus-Minus

The concept of plus-minus to capture player impact is a sensible one. Raw plus-minus, found in NBA box scores, is the net team points while the player is on the court. If a team tends to outscore opponents while a player is on the court, then perhaps the player is driving team success. If you could randomize who players play with and against, with plenty of games for each combination, raw plus-minus would be a nearly perfect measure of player impact. Unfortunately, coaches don't randomize their rotations, general managers don't make random trades, and players can only play so many games. In the real world, raw plus-minus is very biased. It moves with many factors beyond what the player contributes, and it is extremely noisy even in seemingly large samples.

As an example, in the 2023-24 NBA regular season among qualifying players, Kentavious Caldwell-Pope, Payton Pritchard, Luke Kornet, Kenrich Williams, Jusuf Nurkic, Nickeil Alexander-Walker, and Lu Dort all had a higher raw on-court plus-minus per 100 possessions than Stephen Curry, Giannis Antetokounmpo, Luka Doncic, and Devin Booker (source: Basketball Reference play-by-play). While the former are fine players, you would be hard-pressed to find a respected scout or analyst who would call them more impactful than the latter.

Many of the players with a high plus-minus play alongside great players on good teams: Caldwell-Pope next to Nikola Jokic, Payton Pritchard and Luke Kornet on a great Celtics team, and so on. This shows one of the major problems with raw plus-minus. It is blind to context, so it can't see the bias from who players play with or against.

Sample size limits make it harder still to isolate a player's contribution. When a player has a suspiciously high or low raw plus-minus, they often just happened to be on the court during random runs of opponent 3-point shooting that don't reflect true ability. It is tempting to credit the player, but the difference is almost certainly mostly chance, since it has been shown that defenses have little control over opponent 3-point percentage.

Two longstanding, proven techniques help with these problems: regularized adjusted plus-minus (RAPM) and statistical plus-minus (SPM).

The Two Parts of EPM

EPM has two main components:

1. A statistical plus-minus (SPM) model that uses Estimated Skills to estimate a player's contribution per 100 possessions.
2. A regularized adjusted plus-minus (RAPM) calculation that captures impact beyond the stats.

The first step is the starting point for the second, which makes EPM a RAPM calculation with an SPM Bayesian prior. Each method is described below.

Regularized Adjusted Plus-Minus (RAPM)

RAPM is used in the final step to calculate EPM, and it is also used to build the SPM model in the first step. Adjusted plus-minus (APM) came before RAPM as a fix for the context blindness of raw plus-minus. It was first brought to basketball by Dan Rosenbaum to adjust a player's plus-minus for who they play with and against, as well as other factors such as home court advantage and the rubber band effect.

Regularized adjusted plus-minus (RAPM) was a major improvement on APM. Joe Sill introduced it at the 2010 Sloan Sports Analytics Conference (abstract here), where he reported nearly doubling the accuracy of traditional APM. RAPM uses ridge regression, a statistical technique that limits the problems caused by players who frequently play together.

RAPM is calculated with a huge ridge regression model. It can be easier to picture as solving a system of equations: the unknowns are player values, and the equations are team possessions and their outcomes. There are two variables per player, offense and defense, and around 5 million possessions in a 20-season RAPM calculation.

Statistical Plus-Minus (SPM)

The idea of SPM has been around as long as APM, and Dan Rosenbaum also used it in the article linked above. RAPM was a massive upgrade on raw plus-minus but is still noisy. SPM uses player-level stats to stabilize an estimate of impact per 100 possessions.

To build an SPM model, modern metrics use large multi-season samples of RAPM, which minimize the noise, along with player stats from the same seasons. Together these show empirically how each stat relates to player impact. The resulting weights can then be applied to player stats to estimate what their RAPM could be without calculating it. SPM output is interesting on its own if modeled well, but it is limited to what the box score, play-by-play, and tracking data can measure. Much of what matters on offense is measured by player stats, while defensive stats are much more limited. Neil Paine wrote a good summary of SPM. Daniel Myers created Box Plus/Minus (BPM), a fantastic SPM metric with a thorough write-up and a large part of the inspiration behind EPM.

Combining SPM and RAPM

EPM is also inspired by Jeremias Engelmann and Steve Ilardi's Real Plus-Minus (RPM), which combined these two methods to arrive at more accurate player values. RPM used an SPM model as a Bayesian prior in a one-season RAPM calculation called xRAPM, with great results. EPM uses a similar approach, with its own SPM model and a predictive orientation. It is powered by Estimated Skills, player-tracking data, and players' entire careers rather than single seasons.

Estimated Skills

Much of EPM's predictive power comes from stats optimized individually to estimate true skill. Each is a prediction of the stat's most likely value at a point in time. It accounts for how the stat stabilizes over time, the player's career up to that point, and how factors such as age, team and opponent strength, and seasonality affect that particular stat. These are called skills, for example 3-point % skill, or stable 3-point %.

You often hear that a stat needs enough sample before you can trust it, but how much is enough? Each stat stabilizes at a different rate, so some need far more sample than others. Estimated Skills solve the sample size problem for you by working out how much weight each past game deserves for each stat.

For example, if a player shoots 60% on threes over 10 games and 50 attempts, what should you expect in the next game? Not 60%. That is still an impressive run, so how much of it is real? 3-point % skill tells you. In general, 3-point % misleads more than 2-point % in the short term and needs more sample to trust. Knowing how much more matters when comparing players with different shot profiles.

Each stat also responds differently to player age, league-wide trends within a season, home court, back-to-back games, and other factors. For example, age helps predict 3-point % but matters less for how often a player shoots threes. Shooting efficiency is typically lower early in the season and against strong defenses. The biggest driver of a player's next game is their optimized, decay-weighted career performance up to that point, described next, but accounting for these factors improves the prediction.

Each skill comes in a game-agnostic and a game-optimized form, explained under Expected EPM. How skills compare with a season-to-date average is under Prediction Results.

Estimated Skill Methodology

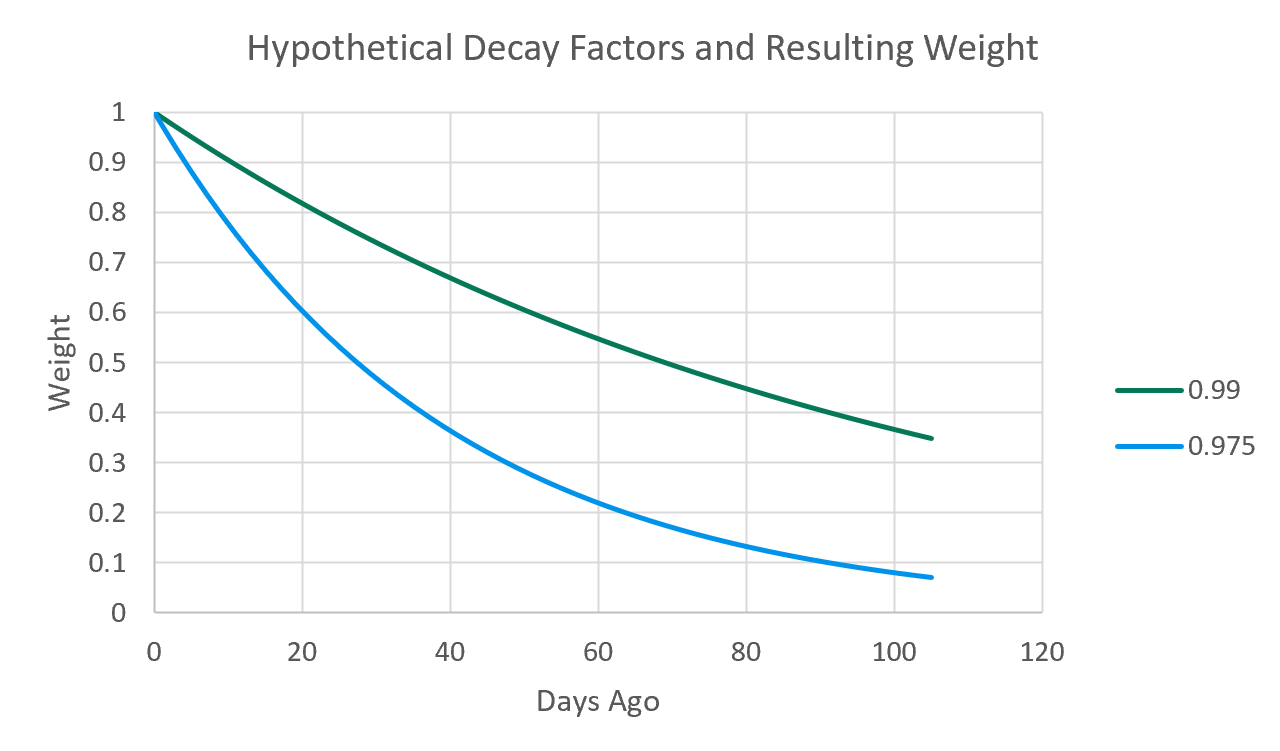
To calculate skills, each stat gets its own predictive model, and each model is tuned with a machine learning optimization algorithm called Differential Evolution. The optimizer finds the weights to give all past games for each stat that best predict each player's next game, given their career up to that point. The weights decay exponentially: the most recent game gets the most weight and older games gradually less, and the optimizer decides how gradual that decay should be.

More specifically, the optimizer sets a decay factor, a number between 0 and 1. Raised to the power of how many days ago a game was, it gives that game's weight. A decay factor of 1 weights all past games equally, and most decay factors are just below 1. This chart shows the decay for several hypothetical decay factors.

Continuing the 3-point % versus 2-point % example, 3-point % needs more sample to stabilize, so it gets a higher decay factor. Depending on the stat, weights count back by days or by possessions. The result is the optimized prediction for every stat, for every player, at every point in time. This approach is inspired by Kostya Medvedovsky's DARKO model.

Expected EPM

Expected EPM is a player's predicted impact per 100 possessions as of a date, using all data before it. It never includes games played on that date. Values exist for every day since the 2001-02 season and update nightly.

Calculating EPM

EPM uses two SPM models, each fit to a multi-season RAPM: a box-score model, and a tracking model that covers defense. The RAPM behind them uses possession-level data, which controls for home court and the rubber band effect, in which teams and players perform worse when ahead and better when behind.

The box-score SPM includes playoffs. Every season from 2023-24 on is outside both models' training data.

The SPM models estimate how much each stat matters to a player's impact when taken together. Applying them to Estimated Skills gives a predictive SPM value for every player on every date.

Those SPM values are the prior for an exponentially decayed RAPM run for every date since 2001-02. Each night's run uses every possession since 2001-02 and weights recent possessions more heavily than older ones, while controlling for home court and the rubber band effect. In all, EPM rests on daily RAPM runs for 5,153 dates across 25 seasons, 2001-02 through 2025-26, one run per date for each flavor of EPM. They cover 32,190 games and about 6.2 million possessions. The result is EPM.

Game-Agnostic and Game-Optimized

Expected EPM and Estimated Skills both come in two flavors:

• Game-agnostic values describe the player independent of opponent or game context. They are the site's main player ratings.
• Game-optimized values predict the player's game on the date. They account for home court, rest, season type, and opponent strength. They also account for the teammates and opponents expected to play, through aggregated skills such as teammates' combined usage or opponents' steal rates. The aggregates are model inputs and aren't shown.

Game-optimized values drive next-game team ratings, game predictions, and box score projections.

Actual EPM

Actual EPM rates a player's season, regular season or playoffs, from the games actually played. Expected EPM predicts what comes next, while Actual EPM describes what happened. It updates nightly.

Actual EPM starts from each player's preseason Expected EPM and lets the season's own results take over as they accumulate. Early-season values lean on the expectation, and late-season values on what actually happened. Playoff ratings lean much more on playoff results, so a strong or weak playoff run shows through.

Because small samples lean on the player's preseason expectation rather than on a replacement-level value, a player with few minutes stays close to what they were expected to be.

Estimated wins (eWins) are the wins a player contributed in a regular season. eWins are the total-production version of EPM, combining efficiency with total playing time.

Use Expected EPM to judge a player's level going forward, and Actual EPM to judge what a player did in a season. See the Actual EPM table.

Playing Time and Availability

Team ratings, game predictions, and box score projections all depend on who plays and for how long. Minutes are predicted for every player in every game and updated frequently as tip-off approaches, using known injuries and official player status. When a player is out, game context informs how their minutes shift to teammates.

Minutes predictions beat the player's season-to-date average by about 15%, the largest gain of any stat (see Prediction Results).

Team Ratings

Team ratings combine player EPM with expected minutes. They are predictive, so a date's rating doesn't include games played that day. Every date has two ratings for each team:

• Next-game rating: the expected lineup for the team's next game, including known injuries.
• Season rating: each player's EPM on the date, applied to the team's season-expected rotation, meaning the average minutes each player is expected to play.

Each rating is computed with both flavors of EPM. The season rating with game-agnostic EPM is the site's primary team rating. All ratings are centred on the league average for each date, so 0 is an average team on that day.

Strength of Schedule

• Offensive SOS (oSOS): the average defensive EPM of the opponents faced, meaning the defenses the team's offense went against.
• Defensive SOS (dSOS): the average offensive EPM of the opponents faced, meaning the offenses the team's defense went against.

Higher values mean a tougher schedule. See Team Ratings.

Game Predictions

Game predictions give each game's predicted score, margin, and home win probability. They use game-optimized team ratings and update with known injuries. Within 30 minutes of tip-off they update more frequently, using official player status and context-aware minutes and EPM values.

The model is retrained before each season using only earlier seasons:

• 2026-27: the current model's first live season.
• 2024-25 and 2025-26: the predictions published before each game at the time, made with the model running then.
• Other seasons: the current model's predictions, each made using only earlier seasons. Predictions for 2001-02 through 2004-05 are the exception: too few earlier seasons exist, so they were not made using only earlier seasons.

Accuracy is under Prediction Results. See predictions for every game on Games.

Box Score Projections

Box score projections give each player's expected line for a game: minutes, points, shooting, rebounds, assists, steals, blocks, and turnovers. Each line combines the player's game-optimized Estimated Skills with expected playing time, so it reflects the teammates and opponents expected to play.

Projections appear on game pages and on Player Performances, next to the actual box score once the game is played.

Estimated Game Production (EGP)

Estimated Game Production (EGP) measures what a player's box score line was worth in a single game, in points of scoring margin. It was inspired by John Hollinger's Game Score and works the same way, as a weighted sum of the box score, but the weights come from a simplified EPM model, so each stat's weight is empirically based. Points, assists, rebounds, steals and blocks add, while shot attempts, free-throw attempts and turnovers subtract, so efficiency counts. A player who records nothing scores 0, and an average appearance of about 22 minutes is worth about 5. It is a measure of what happened, not a rating of the player, so a short, efficient stint keeps every point it earned. Values are scaled by season so games from different eras read on the same scale.

Prediction Results

Figures as of October 2026.

Games

Our live record covers 2024-25 and 2025-26: predictions published before each game, made with the version of the model running at the time. The current model replaced it starting in 2026-27 because of remodeled EPM and Estimated Skills, for which testing indicated potential improvement. The backtest re-predicts 2005-06 through 2023-24 with the current model, retrained before each season using only earlier seasons. The baseline uses each team's opponent-adjusted net rating going into the game, starting from a preseason projection that fades as the season's results come in.

Errors are larger in recent seasons because single games have become harder to predict for every model, the baseline included.

Estimated Skills

Next-game Estimated Skills are fit only on earlier seasons, starting with 2006-07. They beat the player's season-to-date average on every stat: by about 15% for minutes, and by 2–5% for rate stats, where a single game is mostly noise.

Average miss per game, 2023-24 to 2025-26. Percentages are in percentage points, weighted by possessions or attempts.

Backtest and skill results are re-predictions with the current system, fit only on earlier seasons, though some design choices were made with recent seasons in view. Seasons through 2022-23 overlap the SPM training data.

Season Simulations

Every night we simulate the rest of the season 30,000 times. Each game is played out from its prediction, using the projected lineup for that date and expected availability, with a random margin around the predicted spread. Player availability is simulated game by game, and each absence changes team strength through the minutes it redistributes.

The simulation applies the full NBA tiebreaker rules and plays the NBA Cup, the play-in, and best-of-seven playoff series with home court to the better seed. It produces projected wins, seed and play-in odds, odds for each playoff round and the title, Cup odds, and games-played projections for each player. See Season Probabilities.

Data and API

EPM and Estimated Skills are available for every day of basketball since the 2001-02 season. Expected EPM, Estimated Skills, team ratings, Actual EPM, and season simulations update nightly. Game predictions also update more frequently within 30 minutes of tip-off.

API

The same data is available through the API with an API subscription. Version 1 of the API remains available through the 2026-27 season.